DNN 算法推导

0. 写在前面

14 年刚接触 $DNN$ 的时候推导的公式，现在把它放在博客里面，可以方便的给大家参考，也方便自己后面查阅。

2014年夏，一次培训场景，也正是这位同学让我走进了语音识别的方向，同样也正是因为他，让我离开了讯飞，深深的记得当时离开前喊我谈话的时候，问我去哪了，我说去阿里了，他说 去做测试 吗。。。

1. 假设

训练过程分为两个阶段：各层输出的前向计算（正向传播），各层误差的反正传播。下面分别介绍这两个阶段，并给出详细的公式推导过程

假设：

• 输入层：信号$x_{s}$节点数目为$d$，$i = 1,2,\ldots,d$

• 共有6层隐藏层，每层各有$n_{H}$节点

• 输出层：信号$z_{m}$，节点数目为$c$，$m = 1,2,\ldots,c$

• 目标信号$t_{m}$，$m = 1,2,\ldots,c$

2. 正向传播

• $\text{sigmoid}$函数：$f\left( \text{net} \right) = \frac{1}{1 + exp\left( \text{net} \right)}$ ，各隐层激活函数均为$\text{sigmoid}$函数。$hidden1\sim hidden6$层的输入信号定义为$\text{net}^{\left( k \right)},k = 1,2,\ldots,6$，各隐层的输出信号定义为$y^{\left( k \right)},k = 1,2,\ldots,6$

• $\text{output}$层函数$\text{softmax}$：

\[z_{m} = g\left( \text{net}_{m} \right) = \frac{\exp\left( \text{net}_{m} - \operatorname{}\text{net}_{i} \right)}{\sum_{k = 1}^{c}{\exp\left\lbrack \text{net}_{k} - \operatorname{}\text{net}_{i} \right\rbrack}}\]

其中 $net_m$ 表示 $output$ 层第 $m$ 个节点的输入，$z_m$ 表示 $output$ 层第 $m$ 个节点的输出。

根据输入层信号计算出$hidden1$层的输入，$hidden1$层的输出，然后再计算出$hidden2$层的输入和输出，以此类推推出所有隐层的输入和输出。最后我们再根据$hidden6$层的输出计算出$output$层的输入和输出。具体过程如下：

由输入信号计算$hidden1$层的输入和输出：

\[\text{ne}t_{j}^{\left( 1 \right)} = \sum_{i = 1}^{d}{x_{i}w_{\text{ji}}^{\left( 1 \right)}} + b_{j}^{(1)}\] \[y_{j}^{(1)} = f(net_{j}^{\left( 1 \right)})\]

计算$hidden2$层的输入和输出：

\[\text{ne}t_{f}^{\left( 2 \right)} = \sum_{j = 1}^{n_{H}}{y_{j}^{(1)}w_{\text{fj}}^{\left( 2 \right)}} + b_{f}^{(2)}\] \[y_{f}^{(2)} = f(net_{f}^{\left( 2 \right)})\]

$hidden3$层：

\[\text{ne}t_{q}^{\left( 3 \right)} = \sum_{f = 1}^{n_{H}}{y_{f}^{(2)}w_{\text{qf}}^{\left( 3 \right)}} + b_{q}^{(3)}\] \[y_{q}^{(3)} = f(net_{q}^{\left( 3 \right)})\]

$hidden4$层：

\[\text{ne}t_{p}^{\left( 4 \right)} = \sum_{q = 1}^{n_{H}}{y_{q}^{(3)}w_{\text{pq}}^{\left( 4 \right)}} + b_{p}^{(4)}\] \[y_{p}^{(4)} = f(net_{p}^{\left( 4 \right)})\]

$hidden5$层：

\[\text{ne}t_{a}^{\left( 5 \right)} = \sum_{p = 1}^{n_{H}}{y_{p}^{(4)}w_{\text{ap}}^{\left( 5 \right)}} + b_{a}^{(5)}\] \[y_{a}^{(5)} = f(net_{a}^{\left( 5 \right)})\]

$hidden6$层：

\[\text{ne}t_{l}^{\left( 6 \right)} = \sum_{a = 1}^{n_{H}}{y_{a}^{(5)}w_{\text{la}}^{\left( 6 \right)}} + b_{l}^{(6)}\] \[y_{l}^{(6)} = f(net_{l}^{\left( 6 \right)})\]

$\text{output}$层：

\[\text{ne}t_{m}^{\left( 7 \right)} = \sum_{l = 1}^{n_{H}}{y_{l}^{(6)}w_{\text{ml}}^{\left( 7 \right)}} + b_{m}^{(7)}\] \[z_{m} = g(net_{m}^{\left( 7 \right)})\]

下图为DNN前向计算的过程：

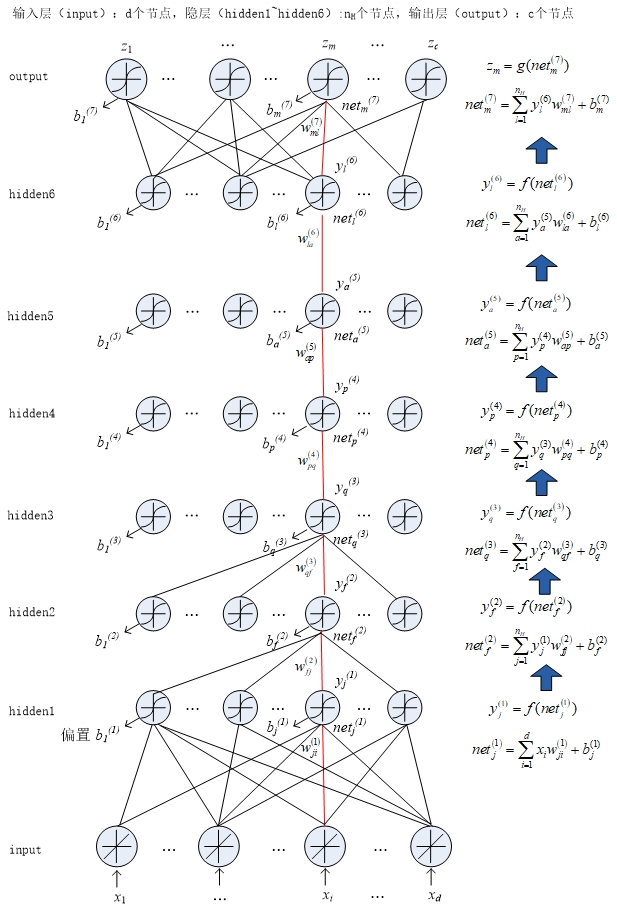
输入的正向传播

3. 反向传播

反向传播是指DNN网络误差的传播，即输出层开始，将每一层的误差传给前一层。

随机梯度下降法

基本思想：定义一个与待定参数有关的误差函数，并通过反复修正有关参数，使得该误差函数尽可能的达到最小状态（极小值）

梯度方向是使得误差函数增长最快的方向，因此为了是的误差最小，我们应该沿着”负”梯度方向走

在DNN中，误差是由输出层和期望输出的差值决定的，即误差函数为：

\[J = \frac{1}{2}\sum_{m = 1}^{c}{(t_m - z_m)^{2}}\]

其中，待定参数是各层的权值$w_{}^{(k)}$，以及偏置$b^{(k)}$。根据梯度下降法，我们可以令：

\[\Delta w^{(k)} = - \eta\frac{\partial J}{\partial w^{(k)}}\] \[\Delta b^{(k)} = - \eta\frac{\partial J}{\partial b^{(k)}}\]

其中$\eta$是学习率。可以分别计算出每一层权值和偏置的增量，从而实现对权值、偏置的更新。下面我们分别推导出各层$w_{}^{(k)}$和$b^{(k)}$的增量，$k = 1,2,…,7$，$s$表示每一层的下标

我们做如下定义：

上误差：

\[e_{s}^{k \uparrow} = \frac{\partial J}{\partial y_{s}^{k}}\]

下误差：

\[e_{s}^{k \downarrow} = \frac{\partial J}{\partial\text{ne}t_{s}^{k}}\]

又因为

\[y_{s}^{k} = f(net_{s}^{k})\]

所以：

\[e_{s}^{k \downarrow} = \frac{\partial J}{\partial\text{ne}t_{s}^{k}} = \frac{\partial J}{\partial y_{s}^{k}} \cdot \frac{\partial y_{s}^{k}}{\partial\text{ne}t_{s}^{k}} = e_{s}^{k \uparrow} \cdot f^{'}(net_{s}^{k})\]

由此，我们开始分别计算每一层的增量

对于输出层有：

\[{\Delta w_{\text{ml}}^{(7)} = - \eta\frac{\partial J}{\partial w_{\text{ml}}^{(7)}} = - \eta\frac{\partial J}{\partial\text{ne}t_{m}^{(7)}} \cdot \frac{\partial\text{ne}t_{m}^{(7)}}{\partial w_{\text{ml}}^{(7)}} = - \eta e_{m}^{(7) \downarrow} \cdot y_{l}^{(6)}}\] \[{\Delta b_{m}^{(7)} = - \eta\frac{\partial J}{\partial b_{m}^{(7)}} = - \eta\frac{\partial J}{\partial\text{ne}t_{m}^{(7)}} \cdot \frac{\partial\text{ne}t_{m}^{(7)}}{\partial b_{m}^{(7)}} = - \eta e_{m}^{(7) \downarrow}}\]

对于$hidden6$有：

\[{\Delta w_{\text{la}}^{(6)} = - \eta\frac{\partial J}{\partial w_{\text{la}}^{(6)}} = - \eta\frac{\partial J}{\partial\text{ne}t_{l}^{(6)}} \cdot \frac{\partial\text{ne}t_{l}^{(6)}}{\partial w_{\text{la}}^{(6)}} = - \eta e_{l}^{(6) \downarrow} \cdot y_{a}^{(5)}}\] \[{\Delta b_{l}^{(6)} = - \eta\frac{\partial J}{\partial b_{l}^{(6)}} = - \eta\frac{\partial J}{\partial\text{ne}t_{l}^{(6)}} \cdot \frac{\partial\text{ne}t_{l}^{(6)}}{\partial b_{l}^{(6)}} = - \eta e_{l}^{(6) \downarrow}}\]

同理可以得出剩余各层的增量：

$\text{hidden}5$：

\[\Delta w_{\text{ap}}^{(5)} = - \eta\frac{\partial J}{\partial w_{\text{ap}}^{(5)}} = - \eta e_{a}^{(5) \downarrow} \cdot y_{p}^{(4)}\] \[\Delta b_{a}^{(5)} = - \eta\frac{\partial J}{\partial b_{a}^{(5)}} = - \eta e_{a}^{(5) \downarrow}\]

$\text{hidden}4$：

\[\Delta w_{\text{pq}}^{(4)} = - \eta\frac{\partial J}{\partial w_{\text{pq}}^{(4)}} = - \eta e_{p}^{(4) \downarrow} \cdot y_{q}^{(3)}\] \[\Delta b_{p}^{(4)} = - \eta\frac{\partial J}{\partial b_{p}^{(4)}} = - \eta e_{p}^{(4) \downarrow}\]

$\text{hidden}3$：

\[\Delta w_{\text{qf}}^{(3)} = - \eta\frac{\partial J}{\partial w_{\text{qf}}^{(3)}} = - \eta e_{q}^{(3) \downarrow} \cdot y_{f}^{(2)}\] \[\Delta b_{q}^{(3)} = - \eta\frac{\partial J}{\partial b_{q}^{(3)}} = - \eta e_{q}^{(3) \downarrow}\]

$\text{hidden}2$：

\[\Delta w_{\text{fj}}^{(2)} = - \eta\frac{\partial J}{\partial w_{\text{fj}}^{(2)}} = - \eta e_{f}^{(2) \downarrow} \cdot y_{j}^{(1)}\] \[\Delta b_{a}^{(5)} = - \eta\frac{\partial J}{\partial b_{a}^{(5)}} = - \eta e_{l}^{(5) \downarrow}\]

而对于$\text{hidden}1$层有：

\[{\Delta w_{\text{ji}}^{(1)} = - \eta\frac{\partial J}{\partial w_{\text{ji}}^{(1)}} = - \eta\frac{\partial J}{\partial\text{ne}t_{j}^{(1)}} \cdot \frac{\partial\text{ne}t_{j}^{(1)}}{\partial w_{\text{ji}}^{(1)}}= - \eta e_{j}^{(1) \downarrow} \cdot x_{i}}\] \[{\Delta b_{j}^{(1)} = - \eta\frac{\partial J}{\partial b_{j}^{(1)}} = - \eta\frac{\partial J}{\partial\text{ne}t_{j}^{(1)}} \cdot \frac{\partial\text{ne}t_{j}^{(1)}}{\partial b_{j}^{(1)}}= - \eta e_{j}^{(1) \downarrow}}\]

由上面的推导可以看出，$k$层的权值增量由$k$层的下误差$e_{s}^{(k) \downarrow}$和$k - 1$层的输出$y_{r}^{(k - 1)}$来决定，$k$层的偏置增量由$k$层的下误差$e_{s}^{(k) \downarrow}$决定。

\[\Delta w_{\text{sr}}^{(k)} = - \eta\frac{\partial J}{\partial w_{\text{sr}}^{(k)}} = - \eta e_{s}^{(k) \downarrow} \cdot y_{r}^{(k - 1)}\] \[\Delta b_{j}^{(\operatorname{k})} = - \eta\frac{\partial J}{\partial b_{j}^{(\operatorname{k})}} = - \eta e_{j}^{(\operatorname{k}) \downarrow}\]

其中$k = 2,3,…,7$，$s,r$分别表示$k$层和$k - 1$层的下标，且$s,r \in \lbrack 1,n_{H}\rbrack$。注意对于$\text{hidden}1$层，其权值增量由下误差$e_{j}^{(1) \downarrow}$和输入$x_{i}$决定，偏置增量仅与下误差$e_{j}^{(1) \downarrow}$有关。即：

\[\Delta w_{\text{ji}}^{(1)} = - \eta e_{j}^{(1) \downarrow} \cdot x_{i}\] \[\Delta b_{j}^{(1)} = - \eta e_{j}^{(1) \downarrow}\]

到此我们已经知道了各层权值增量，偏置增量和下误差的关系。下面我们就该计算每一层的下误差的大小。首先我们推导下输出层的下误差$e_{m}^{(7) \downarrow}$的大小，过程如下：

\[e_{m}^{(7) \uparrow} = \frac{\partial J}{\partial z_{m}} = - (t_m - z_m)\]

划简得：

\[e_{m}^{(7) \downarrow} = \frac{\partial J}{\partial\text{ne}t_{m}^{(7)}} = e_{m}^{(7) \uparrow} \cdot g'(net_{m}^{(7)})\]

继续计算$hidden6$的误差如下：

\[{e_{l}^{(6) \uparrow} = \frac{\partial J}{\partial y_{l}^{(6)}} = \frac{\partial J}{\partial\text{ne}t_{m}^{(7)}} \cdot \frac{\partial\text{ne}t_{m}^{(7)}}{\partial y_{l}^{(6)}} = e_{m}^{(7) \downarrow} \cdot w_{\text{ml}}^{(7)}}\] \[e_{l}^{(6) \downarrow} = \frac{\partial J}{\partial\text{ne}t_{l}^{(6)}} = e_{l}^{(6) \uparrow} \cdot f'(net_{l}^{(6)})\]

同理我们可以推出各层的上下误差，即：

\[e_{s}^{(\operatorname{k}) \uparrow} = \frac{\partial J}{\partial y_{s}^{(\operatorname{k})}}\] \[e_{s}^{(\operatorname{k}) \downarrow} = \frac{\partial J}{\partial\text{ne}t_{s}^{(\operatorname{k})}} = e_{s}^{(\operatorname{k}) \uparrow} \cdot f'(net_{s}^{(k)})\]

其中，$k = 1,2,…,6$，s表示当$k$前层的下标，r表示$k + 1$层的下标

上面两个公式可以看出，每层的上误差都和上一层的下误差以及他们这两层之间的权值w有关，而每一层的下误差则又和本身的上误差有关。因此只要计算出最后一层（输出层）的上误差，我们就可以分别推导出各层的上下误差。这个过程是从输出层往输入层的迭代推导，即误差的反向传播。下图我们给出误差反传的整个过程

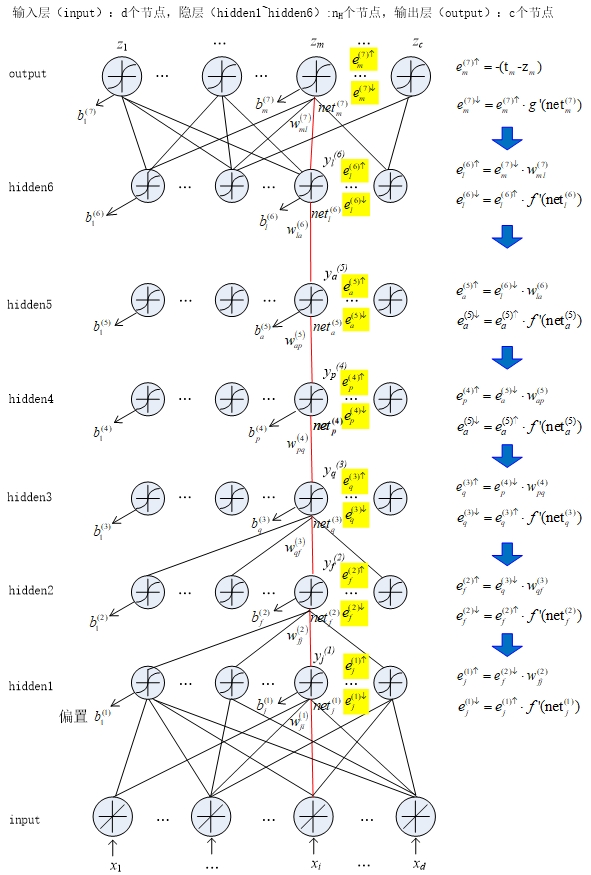
误差反向传播

至此，DNN的前向计算和误差反传过程介绍完毕。最后我们就可以对权值和偏差进行更新操作了，矫正更新量为：

\[\Delta w_{\text{sr}}^{(k)} =(1-m)*\Delta w_{\text{sr}}^{(k)} + m* \Delta \overset{\land}{w}_{\text{sr}}^{(k)}\] \[\Delta b_{\text{s}}^{(k)} =(1-m)*\Delta b_{\text{s}}^{(k)} + m* \Delta \overset{\land}{b}_{\text{s}}^{(k)}\]

其中，$k = 1,2,…,7$，$\Delta\overset{\land}{w}$表示上一次更新时的$\text{Δw}$值。$\Delta\overset{\land}{b}$表示上一次更新时$\text{Δb}$的值。$m$是修正因子。得到矫正更新量后，就可以进行权值和偏置的更新了

\[w_{\text{sr}}^{(k)} = w_{\text{sr}}^{(k)} + \Delta w_{\text{sr}}^{(k)}\] \[b_{s}^{(k)} = b_{s}^{(k)} + \Delta b_{s}^{(k)}\]

最后我们将前向计算和反向传播的全过程重现一遍，见下图

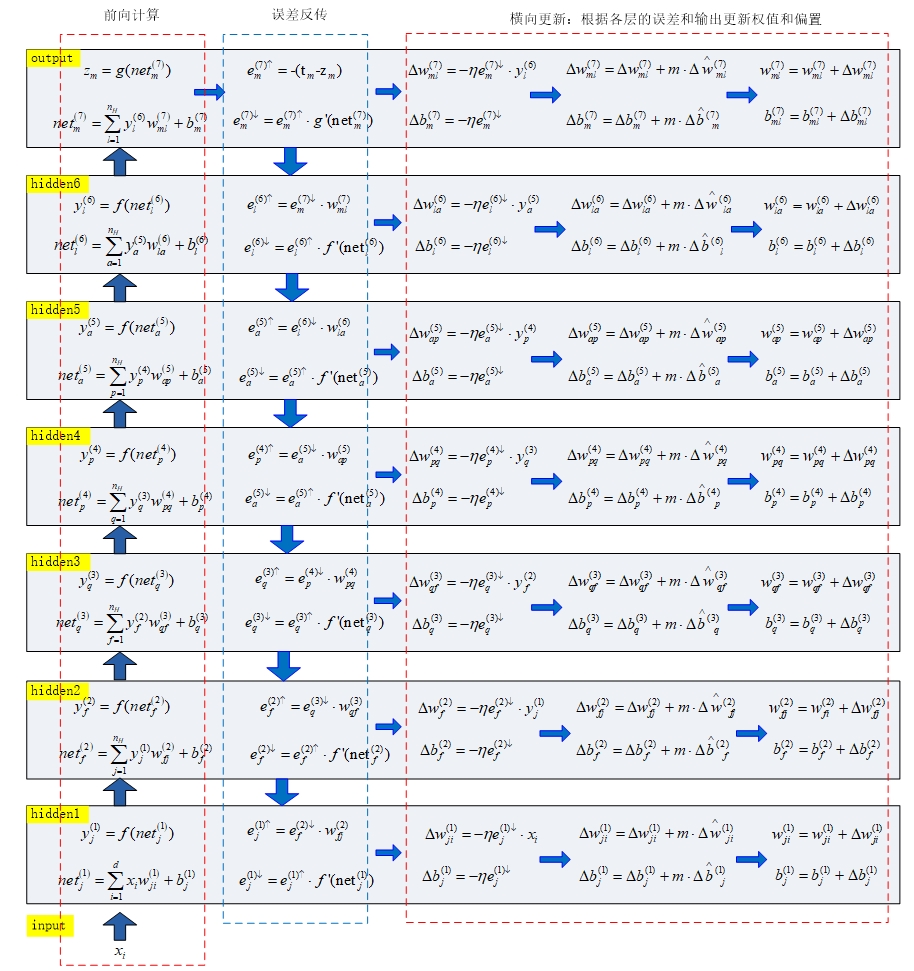
DNN前向计算、反向误差传播及更新

4. DNN在GPU上的实现

以上推导了含有6个隐层的DNN网络的前向计算、反向误差传播，以及权值更新的全过程。上述推导过程是针对一个样本进行的，下面我们给出在GPU上使用N个样本同时进行DNN训练的流程

假设：

• 样本数目：N

• 输入层：信号$x_{i}$，节点数目为$d$，故$i = 1,2,..,d$

• 共有6层隐藏层，每层各有$n_{H}$个节点

• 输出层：信号$z_{m}$，节点数目为$c$，$m = 1,2,..,c$

• 目标信号$t_{m}$，$m = 1,2,..,c$

训练流程如下：

• 从内存中读取N个样本{$X_1,X_2,…,X_N$}，每个样本d维，共d*N个浮点数。将这些数从内存复制到GPU内存中。在实际任务中一般假设N=1024,d=440，每个float的取值范围是(-100，100)

• 计算$\text{hidden}1$层的输入，

\[\text{ne}t_{k,j}^{\left( 1 \right){\sum_{i = 1}^{d}{x_{k,i}w_{\text{ji}}^{\left( 1 \right)}}}_{j}^{(1)}}\]

$k = 1,2,…,N$表示样本的标号。用矩阵表示为：

\[\text{NE}T^{\left( 1 \right)} = XW^{\left( 1 \right)} + B^{\left( 1 \right)}\]

其中$\text{NE}T^{\left( 1 \right)}$为$N*n_H$ 的矩阵

\[\text{NE}T^{(1)} = \begin{bmatrix} \text{ne}t_{1,1}^{(1)} & \text{ne}t_{1,2}^{(1)} & \text{...} & \text{ne}t_{1,n_H}^{(1)} \\ \text{ne}t_{2,1}^{(1)} & \text{ne}t_{2,2}^{(1)} & \text{...} & \text{ne}t_{2,n_H}^{(1)} \\ \text{...} & \text{...} & \text{...} & \text{...} \\ \text{ne}t_{N,1}^{(1)} & \text{ne}t_{N,2}^{(1)} & \text{...} & \text{ne}t_{N,n_H}^{(1)} \\ \end{bmatrix}\]

$X$为$N*d$的矩阵

\[X = \begin{bmatrix} x_{1,1} & x_{1,2} & \text{...} & x_{1,d} \\ x_{2,1} & x_{2,2} & \text{...} & x_{2,d} \\ \text{...} & \text{...} & \text{...} & \text{...} \\ x_{N,1} & x_{N,2} & \text{...} & x_{N,d} \\ \end{bmatrix}\]

$W^{\left( 1 \right)}$为$d*n_H$的矩阵

\[W^{(1)} = \begin{bmatrix} w_{1,1}^{(1)} & w_{1,2}^{(1)} & \text{...} & w_{1,n_H}^{(1)} \\ w_{2,1}^{(1)} & w_{2,2}^{(1)} & \text{...} & w_{2,n_H}^{(1)} \\ \text{...} & \text{...} & \text{...} & \text{...} \\ w_{d,1}^{(1)} & w_{d,2}^{(1)} & \text{...} & w_{d,n_H}^{(1)} \\ \end{bmatrix}\]

$B^{\left( 1 \right)}$也是$N*n_H$的矩阵

\[B^{(1)} = \begin{bmatrix} b_{1,1}^{(1)} & b_{1,2}^{(1)} & \text{...} & b_{1,n_H}^{(1)} \\ b_{2,1}^{(1)} & b_{2,2}^{(1)} & \text{...} & b_{2,n_H}^{(1)} \\ \text{...} & \text{...} & \text{...} & \text{...} \\ b_{N,1}^{(1)} & b_{N,2}^{(1)} & \text{...} & b_{N,n_H}^{(1)} \\ \end{bmatrix}\]

• 计算 $\text{hidden}1$ 层的输出，$y_{k,j}^{(1)} = f(net_{k,j}^{\left( 1 \right)})$

\[Y^{(1)} = \begin{bmatrix} f(net_{1,1}^{(1)}) & f(net_{1,2}^{(1)}) & \text{...} & f(net_{1,n_H}^{(1)}) \\ f(net_{2,1}^{(1)}) & f(net_{2,2}^{(1)}) & \text{...} & f(net_{2,n_H}^{(1)}) \\ \text{...} & \text{...} & \text{...} & \text{...} \\ f(net_{N,1}^{(1)}) & f(net_{N,2}^{(1)}) & \text{...} & f(net_{N,n_H}^{(1)}) \\ \end{bmatrix}\]

• 计算$\text{hidden}2$层的输入值

\[\text{NE}T^{\left( 2 \right)} = Y^{(1)}W^{\left( 2 \right)} + B^{\left( 2 \right)}\]

其中$\text{NE}T^{\left( 2 \right)}$为$N \cdot n_H$ 的矩阵，$Y^{\left( 1 \right)}$为$N \cdot n_H$ 的矩阵，$W^{\left( 2 \right)}$为$n_H\cdot n_H$的矩阵，$B^{\left( 2 \right)}$也是$N \cdot n_H$的矩阵

• 计算$\text{hidden}2$层的输出值 $y_{k,j}^{(2)_{k,j}^{\left( 2 \right)}}$。重复步骤三和步骤四直到计算出所有层的输入和输出值（总共6个隐层）

• 计算$\text{output}$层的输入值，$Z = Y^{(6)}W^{\left( 7 \right)} + B^{\left( 7 \right)}$，其中$Z$为$N\cdot c$ 的矩阵，$Y^{\left( 6 \right)}$为$N\cdot n_H$ 的矩阵，$W^{\left( 7 \right)}$为$n_H\cdot c$的矩阵，$B^{\left( 7 \right)}$也是$N \cdot c$的矩阵。

• 计算$\text{output}$层的输出值$z_{m} = g(net_{m}^{(7)})$

• 计算$\text{output}$层的上误差

\[e_{k,m}^{(7) \uparrow} = - (t_{k,m}\mathrm{-}\mathrm{z}_{k,m})\]

并由此计算$\text{output}$层的下误差

\[e_{k,m}^{(7) \downarrow} = e_{k,m}^{(7) \uparrow} \cdot g'(net_{k,m}^{(7)})\]

• 计算$\text{hidden}6$层的上误差$e_{k,l}^{(6) \uparrow} = e_{k,m}^{(7) \downarrow} \cdot w_{\text{ml}}^{(7)}$，即$E_{}^{(6) \uparrow} = E_{}^{(7) \downarrow} \cdot W^{(7)T}$。

• 计算$\text{hidden}6$层的下误差

\[e_{k,l}^{(6) \downarrow} = e_{k,l}^{ {(6)}\uparrow net_{k,l}^{(6)} }\]

• 重复上述2个步骤计算其余各隐层的上下误差。直到计算到$\text{hidden}1$层为止

• 计算权值和偏置值的增量

\[\Delta w_{\text{ji}}^{(\operatorname{s})} = - \eta\sum_{k = 1}^{N\sum}e_{k,j}^{(\operatorname{s}) \downarrow_{i}^{(\operatorname{s} - 1)}}\] \[\Delta b_{j}^{(\operatorname{s})} = - \eta\sum_{k = 1}^{N\sum}e_{k,j}^{(\operatorname{s}) \downarrow}\]

$s$表示层数$s = 2,3,…,7$ ，$j$ 表示$s$层的下标，$i$表示$s - 1$层的下标。对于$\text{hidden}1$层有：

\[\Delta w_{\text{ji}}^{(1)} = - \eta\sum_{k = 1}^{N}{e_{k,j}^{(1) \downarrow} \cdot x_{i}}\] \[\Delta b_{j}^{(1)} = - \eta\sum_{k = 1}^{N}e_{k,j}^{(1) \downarrow}\]

$j$ 表示$\text{hidden}1$层的下标，$i$表示$\text{input}$层的下标

• 矫正更新量

\[\Delta w_{\text{ji}}^{(k)} =\Delta w_{\text{ji}}^{(k)} + m \cdot \Delta \overset{\land}{w}_{\text{ji}}^{(k)}\] \[\Delta b_{\text{j}}^{(k)} =\Delta b_{\text{j}}^{(k)} + m\cdot \Delta \overset{\land}{b}_{\text{j}}^{(k)}\]

其中$k = 1,2,…,7$ 和 $ \Delta \overset\land w_{ji}^{(k)} $ 表示上一次更新时的 $\Delta w_{ji}^{(k)}$ 值, $\Delta \overset\land b_{j}^{(k)}$ 表示上一次更新时的 $\Delta b_{j}^{(k)}$ 值

• 更新权重和偏置值

\[\begin{matrix} w_{\text{ji}}^{(k)} = w_{\text{ji}}^{(k)} + \Delta w_{\text{ji}}^{(k)} \\ b_{j}^{(k)} = b_{j}^{(k)} + \Delta b_{j}^{(k)} \\ \end{matrix}\]

其中 $k = 1,2,…,7$

• 重复所有步骤直到所有样本都已经训练完毕