0. 写在前面
做算法的同学,估计大多数都有这样的感受,模型训练好了,在某一个测试集上测试效果不错,换了一个,结果差强人意,想想都知道,因为训练集和测试集不匹配呗,神经网络没有见过呗,所以你给她一个新的东西,当然不认识了
为了解决或抑制这样的问题,我谷歌了一下在声纹领域的领域迁移方案,看到了讯飞,google的一些文章,挑了一篇比较靠谱的记录下来,特地给大家分享。还是惯例,每篇博文都想展示下自己的影子 :)

2015年10月19日,快要离开待了一年多的讯飞时,拍的,留作纪念
1. 背景
去年,大部分时间都在做声纹POC(客户招标,几个厂家一起PK效果,我们参与其中),我们总共经历了十几次银行或公安的POC,虽然有一半以上取得第一名,但是过程是相当艰辛。几乎每次都需要到客户那精细的处理数据,精标部分数据,重新训练调优模型,周期比较长,投入的人力也比较大。归根结底是客户那每次POC的数据特点都不相同,有来自各客户的业务数据,有来自竞品提供的测试数据,他们的信道特点,压缩解码算法,环境背景,说话的内容领域等等各有不同程度的差异,我们没有一个统一的模型去覆盖或胜任各类测试场景,所以需要利用各种方法去调优模型
受到 $《Unsupervised\ Domain\ Adaptation\ by\ Backpropagation》$ 论文的启发,我们决定尝试设计类似的网络结构,加入对抗学习的策略,最大化屏蔽不同领域的差异,提高说话人标签预测的准确率,通过客户提供的大量未标注的数据来对我们的模型进行快速的调优,这样就可以减少人力的投入,缩短POC周期,进而取得更好的成绩
2. 方案介绍
我们设计的领域对抗方案,实质是最大化消除不同信道带来的影响,提取不同信道的不变量,即说话人本身的特征。基本思想是设计和训练三个学习器:生成器 G 和分类器 D1 D2 ,基于 G 生成新的样本 f,基于 D1 从说话人的角度去分辨 f,基于 D2 从领域的角度去分辨f(可以认为我们自己的数据是属于一个领域,待测试的客户数据是属于另外一个领域),通过 G 和 D1 D2 之间的博弈相互提升 G 和 D1 D2 的性能。总之是基于共性特征提取的思想,具体包括如下2个方面:
-
双支路对抗架构:第一条支路包括了特征提取器(feature extractor)和标签预测器(label predictor),构成了一个标准的前馈结构。第二条支路共享了第一条支路的特征提取器,通过一个梯度反向层(gradient reversal layer)接入一个领域分类器(domain classifier),因此其关键是在反向BP训练时,梯度被乘以一个负的常数,从而引入了对抗。
-
对抗训练效应:如果不加入梯度反向层,双支路架构就是个标准的多功能网络,同时降低标签预测和领域分类的损失。但是因为架构中加入了对抗用的梯度反相器,训练结果是“即使两个领域有差别,双支路对抗网络在特征提取器的输出几乎是相同的”。于是,特征提取器(feature extractor) 输出的是与领域无关的不变量。
具体框架如下图所示:
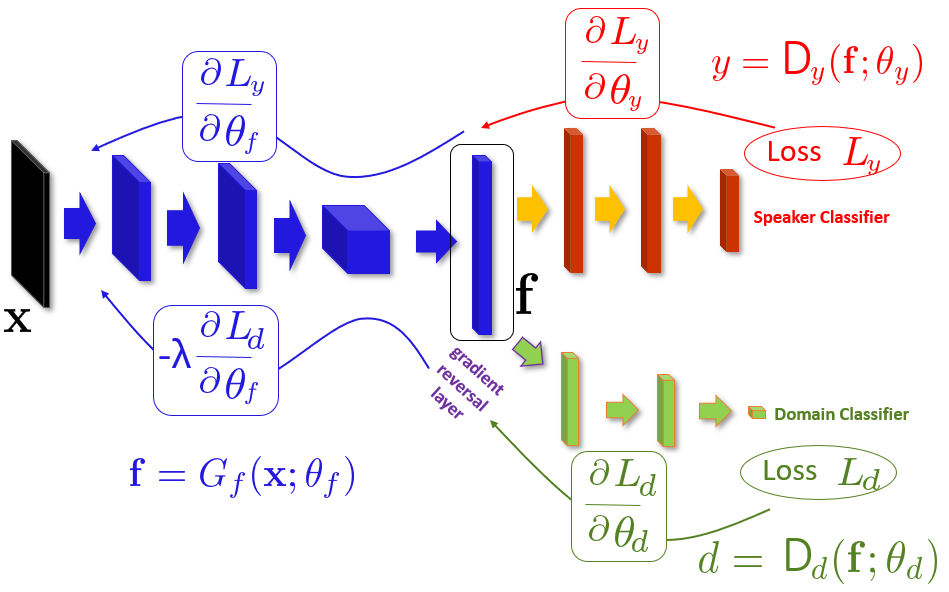
3. 模型解析
我们假设模型的输入样本为 $ x\in X $ , $ X $ 表示某种分布的空间,输出的标签 $ y $ 来源于另外一个空间 $ Y $ ,并且 $ Y $ 是一个有限的集合 $ (Y={1,2,3,…L}) $ ,进一步我们假设两种分布即源分布(source distribution) $ S(x,y) $ 与目标分布(target distribution) $ T(x,y) $ ,也分别代表着源领域与目标领域,这两个分布是复杂且未知的,但是他们是相似的,可以假想为 $ S $ 是 $ T $ 的经过某种 $ shift $ 得到的
我们的终极目标是预测目标领域 $ T $ 的输入样本 $ x $ 的标签 $ y $ 。我们在训练的时候,可以接触到大量的样本数据 $ {x_1,x_2,x_3…x_N} $ ,他们分别来自 $ S(x) $ 与 $ T(y) $ 。我们用二值化的变量 $ d_i $ 表示领域标签,比如对于第 $ i $ 个输入样本,如果它来自源领域,那么我们记为 $ (x_i\sim S(x)if\ d_i=0) $ ,如果来自目标领域则记为 $ (x_i\sim T(x)if\ d_i=1) $ 。在训练的时候,我们知道 $ d_i=0 $ 对应的标签 $ y_i\in Y $ ,但是对于 $ d_i=1 $ 对应的标签 $ y_i\in Y $ 我们就不知道了,在测试的时候也是一样的
现在我们设计一个前馈的神经网络框架,对于输入 $ x $ 来预测它的标签 $ y_i\in Y $ 以及领域标签 $ d\in {0,1} $ 。我们将这个映射关系拆解成3个部分,第一个部分是特征提取器 $ G_f $ ,将输入 $ x $ 映射为 $ D $ 维的向量 $ f\in R^D $ ,这部分包括若干前向层,其中涉及到的参数我们统称为 $ \theta_f $ ,第二部分将 $ f $ 映射到标签 $ y $ 的分类器,我们称为 $ D_y $ ,涉及到的参数我们统称为 $ \theta_y $ ,第三部分将 $ f $ 映射到领域 $ d $ 的分类器,我们称为 $ D_d $ ,涉及到的参数我们统称为 $ \theta_d $ ,如上图所示
在训练的过程中,我们致力于降低标签预测的损失(对于有标签的数据,即源数据),通过优化特征提取的参数 $ \theta_f $ 以及标签分类器的参数 $ \theta_y $ ,这样的话,我们就可以确保在源数据上, $ f $ 具备可分辨性,并且预测标签的效果也不错
与此同时,我们也想让 $ f $ 与领域无关,即
\[S(f)=\{G_f(x;\theta_f)| x\sim S(x)\}\]与
\[T(f)=\{G_f(x;\theta_f)| x\sim T(x)\}\]两者分布很相似,在 $ covariate\ shift $ (Shimodaira,2000)的假设下,我们也可以得到这样的结论,目标领域的预测准确率可以达到源领域预测同样的效果。但是衡量 $ S(f) $ 与 $ T(f) $ 的差异是异常艰巨的,因为 $ f $ 是一个高维的向量,并且在学习的过程不断变化。但是有个方法就是观察领域分类器 $ D_d $ 的损失,它是 $ f $ 的分布的另外一个间接的表现。即两者分布约相似, $ D_d $ 的损失就越大。如下图所示,蓝色点与红色点各代表一个领域的样本数据,左边分布具有明显的差异性,右边差异性比较小,我们的期望就是达到右边图的状态。另外我们也可以推理得到,要达到右边的分布的话,务必使 $ D_d $ 的损失朝着增大的方向调整
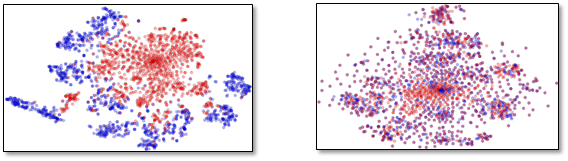
因此我们在训练的时候,为了得到领域无关的 $ f $ ,我们得优化 $ \theta_f $ 使得 $ D_d $ 的损失不断增大,与此同时相应的 $ \theta_d $ 使得 $ D_d $ 的损失不断减小, $ \theta_y $ 使得 $ D_y $ 的损失不断减小,因此,我们设计如下的公式:
\[\begin{align} E(\theta_f,\theta_y,\theta_d) &=\sum_{i=1...N;d_i=0}L_y(D_y(G_f(x_i;\theta_f);\theta_y),y_i)-\lambda\sum_{i=1...N}L_d(D_d(G_f(x_i;\theta_f);\theta_d),d_i) \\ & =\sum_{i=1...N;d_i=0}L_y^i(\theta_f,\theta_y)- \sum_{i=1...N}L_d^i(\theta_f,\theta_d)\\ \end{align}\]其中 $ L_y(.,.) $ 是标签分类器的损失, $ L_d(.,.) $ 是领域分类器的损失, $ L_y^i,L_d^i $ 对应第 $ i $ 次的训练样本的损失,所以我们最终要得到的参数 $ \hat\theta_f,\hat\theta_y,\hat\theta_d $ ,如下
\[\begin{align} (\hat\theta_f,\hat\theta_y) &=arg \min_{\theta_f,\theta_y}E(\theta_f,\theta_y,\hat \theta_d) \\ \hat\theta_d& =arg \max_{\theta_d}E(\hat\theta_f,\hat\theta_y,\theta_d)\\ \end{align}\]我们可以看出 $ \theta_d $ 是最小化领域分类损失的, $ \theta_y $ 是最小化标签分类损失的,而 $ \theta_f $ 是最小化标签分类损失,最大化领域分类损失的,这样从而得到领域无关的 $ f $ , $ \lambda $ 调节着两者目标的损失
4. 梯度反向
根据微分的连式法则,我们从 $ E(\theta_f,\theta_y,\theta_d) $ 可以得到梯度的更新公式:
\[\begin{align} \theta_f &\leftarrow \theta_f-\mu(\frac{\partial L_y^i}{\partial \theta_f}-\lambda \frac{\partial L_d^i}{\partial \theta_f}) \\ \theta_y &\leftarrow \theta_y-\mu\frac{\partial L_y^i}{\partial \theta_y} \\ \theta_d &\leftarrow \theta_d-\mu\frac{\partial L_d^i}{\partial \theta_d} \\ \end{align}\]其中 $ \mu $ 是学习率,这里的更新方式与随机梯度下降很类似,但是有个区别就是 $ -\lambda $ 因子,如果没有这个因子的话,那么提取出来的 $ f $ 将变成领域相关了,不同领域的 $ f $ 将不再相似。如果直接实现上述的反向因子比较困难。我们可以定义一个梯度反向层(gradient reversal layer(GRL)),这层本身不包括神经网络参数,只有一个超参数 $ \lambda $ ,不随网络更新而改变。在前向传递过程中,GRL就相当于一个单位变换,反向更新中,GRL相当于将后面传递过来的梯度乘以 $ -\lambda $ ,在传给前一层。如上面框架图所示,GRL放置在 $ G_f $ 与 $ D_d $ 之间。我们从数学角度出发,可以用伪方程 $ R_\lambda(x) $ 表示GRL的前后向行为:
\[\begin{align} R_\lambda(x) & = x\\ \frac{dR_\lambda}{dx} &=-\lambda I \\ \end{align}\]其中 $ I $ 是单位阵,因此原先的 $ E(\theta_f,\theta_y,\theta_d) $ ,可以修改为:
\[\hat E(\theta_f,\theta_y,\theta_d) =\sum_{i=1...N;d_i=0}L_y(D_y(G_f(x_i;\theta_f);\theta_y),y_i)+\sum_{i=1...N}L_d(D_d(R_\lambda(G_f(x_i;\theta_f));\theta_d),d_i)\]整个网络训练完成后, $ D_y(G_f(x_i;\theta_f);\theta_y) $ 就可以用来预测目标领域的标签了
5. 实验说明
我们采用开源代码库 jvanvugt ,经过加工改造,搭建出说话人识别训练框架,进行声纹识别实验,以SRE16的egs为基础,尝试上述Domain Adversarial Neural Networks(DANN)的效果。特征输入是23维的MFCC,并进行CMVN规整,同时加上能量的 VAD,通过 DANN 网络, $ D_y $ 节点个数 9xxx, $ D_d $ 节点个数 2,准则是 CE。基本的网络框架大致如下:
self.feature_extractor = torch.nn.Sequential(
nn.Conv1d(input_dim, 512, 5),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Conv1d(512, 512, 3, dilation=2),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Conv1d(512, 512, 3, dilation=3),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
)
self.xvector_extractor = torch.nn.Sequential(
nn.Conv1d(512, 512, 1),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Conv1d(512, 1500, 1),
nn.BatchNorm1d(1500, track_running_stats=True, affine=False),
nn.LeakyReLU(),
StatsLayer(),
nn.Linear(3000, 512),
)
self.classifier = torch.nn.Sequential(
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Linear(512, 512),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Linear(512, out_dim),
)
self.discriminatorGRL = torch.nn.Sequential(
GradientReversalLayer(),
nn.Conv1d(512, 512, 1),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Conv1d(512, 1500, 1),
nn.BatchNorm1d(1500, track_running_stats=True, affine=False),
nn.LeakyReLU(),
StatsLayer(),
nn.Linear(3000, 512),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Linear(512, 512),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Linear(512, 512),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Linear(512, 1),
)
self.discriminator = torch.nn.Sequential(
nn.Conv1d(512, 512, 1),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Conv1d(512, 1500, 1),
nn.BatchNorm1d(1500, track_running_stats=True, affine=False),
nn.LeakyReLU(),
StatsLayer(),
nn.Linear(3000, 512),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Linear(512, 512),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Linear(512, 512),
nn.BatchNorm1d(512, track_running_stats=True, affine=False),
nn.ReLU(),
nn.Linear(512, 1),
)
6. 数据说明
训练数据
source: SRE05 SRE06 SRE08 如下 (挑选了一些):
| data | utt | spk | female |
|---|---|---|---|
| sre05 | 2764 | 719 | 519 |
| sre06 | 18320 | 2227 | 1683 |
| sre08 | 23635 | 7871 | 4946 |
target: home_made(业务数据,也是我们要测试的数据)
| data | utt | spk | female |
|---|---|---|---|
| home_made_enroll | 5890 | 1001 | - |
| home_made_test | 851 | 851 | - |
注册与测试数据如下:
| data | utt | spk | female |
|---|---|---|---|
| home_made_enroll | 5890 | 1001 | - |
| home_made_test | 851 | 851 | - |
7. 实验结果
| Model | Size | home_made/EER | RTF |
|---|---|---|---|
| xvector | 27M | 6.991% | 0.0129 |
| DANN | 25M | 6.161% | 0.0114 |
8. 实验结论
在声纹识别上也取得了小幅度的提升,而且速度更快了,模型更小了,不过还是需要在更多的不同测试集上做充分的验证,才可以得出比较靠谱的结论
9. 参考文献
[1] Ganin & Lemptsky,Unsupervised Domain Adaptation by Backpropagation (2014)
[2] Shimodaira, Hidetoshi. Improving predictive inference under covariate shift by weighting the log-likelihood function. Journal of Statistical Planning and Inference, 90(2):227–244, October 2000.
[3] Daniel Povey, Gaofeng Cheng, Yiming Wang, Ke Li, Hainan Xu, Mahsa Yarmohamadi, and Sanjeev Khudanpur, “Semi-orthogonal low-rank matrix factorization for deep neural networks,” in Proceedings of INTERSPEECH, 2018.
[4] R. Prabhavalkar, O. Alsharif, A. Bruguier, and I. McGraw, “On the compression of recurrent neural networks with an application to LVCSR acoustic modeling for embedded speech recognition,” CoRR, vol. abs/1603.08042, 2016.
[5] J. Xue, J. Li, and Y. Gong, “Restructuring of deep neural network acoustic models with singular value decomposition.” in Interspeech, 2013, pp. 2365–2369.
[6] K. J. Han, S. Hahm, B.-H. Kim, J. Kim, and I. Lane, “Deep learning-based telephony speech recognition in the wild,” in Proc. Interspeech, 2017, pp. 1323–1327.

路过的朋友,如果感觉文章对你有启发,能否微信扫一扫,随意打个赏
(如果需要转载,请注明作者和出处 呐喊的少年)
Post Directory
